ARCqK published in Mathematical Programming

I am thrilled to share that the article Scalable adaptive cubic regularization methods has been published in the journal Mathematical Programming, Series A. This has been a really exciting journey with my co-authors Jean-Pierre Dussault and Dominique Orban on this really exciting work that I hope will help explore the numerical possibilities of ARC methods. The proposed implementation is a perfect fit for large-scale application as it solves the subproblem inexactly and only required Hessian-vector products, so no need to evaluate and store the Hessian matrix. As usual, the code has been done in Julia and is available in the folder paper in the Github repository AdaptiveRegularization.jl. Full text published version available from here, enjoy!

Unconstrained Optimization

We consider unconstrained optimization problems of the form \(\underset{x \in \mathbb{R}^n}{\text{minimize}} f(x)\) where $f$ is a twice continuously differentiable function, and its Hessian is Lipschitz continuous. The aim is to study iterative algorithms that converges to a first or second-order stationary points.

A classical approach in this context is to use trust-region method, which is a very robust approach. The Julia package JSOSolvers.jl implements two of such approach, TRON and TRUNK. The book Trust region methods by Conn, Gould, and Toint is a must.

Adaptive Cubic Regularization (ARC)

ARC algorithms, recently explored by Cartis, Gould, and Toint (2011a) and Cartis, Gould, and Toint (2011b) are closely related to trust region methods in that steps are computed by solving a sequence of regularized subproblems. A major theoretical appeal of ARC over TR methods is their optimal worst-case complexity property. Whereas the number of function evaluations required to reach a point $x$ for which $|\nabla f(x)|\le\epsilon$ is $O(\epsilon^{-2})$ for TR, which is no better than steepest descent that number is $O(\epsilon^{-3/2})$ for ARC.

How We Do It?

The standard approach consists in performing aniterative search for the shift akin to solving the secular equation in trust-region methods. Such search requires computing the Cholesky factorization of a tentative shifted Hessian at each iteration, which limits the size of problems that can be reasonably considered. In this article, we propose a scalable implementation of ARC named ARCqK in which we solve a set of shifted systems concurrently by way of an appropriate modification of the Lanczos formulation of the conjugate gradient (CG) method. At each iteration of ARCqK to solve a problem with $n$ variables, a range of $m ≪ n$ shift parameters is selected. The CG variant only requires one Hessian-vector product and one dot product per iteration, independently of $m$. Solves corresponding to inadequate shift parameters are interrupted early. All shifted systems are solved inexactly. Such modest cost makes our implementation scalable and appropriate for large-scale problems.

Numerical Results

The numerical results on CUTEst test problems presented in Dolan and Moré performance profile, with respect to the elapsed time, are comparing:

• ARCqK with the implementation of ARC done in Fortran in the library GALAHAD;
• ARCqK with a classical Steihaug-Toint trust-region method implemented in Julia with the same scheme on problems with $\geq 1000$ variables. More details are given in the article, but overall it shows good prospect for ARCqK as the algorithm is both fast and robust.

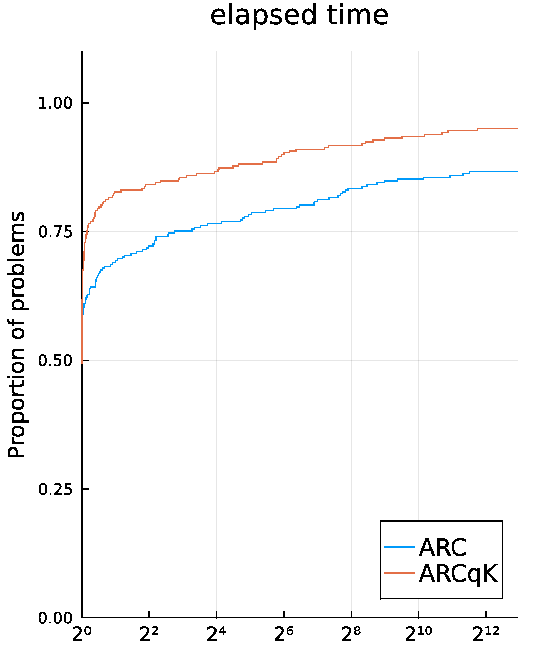
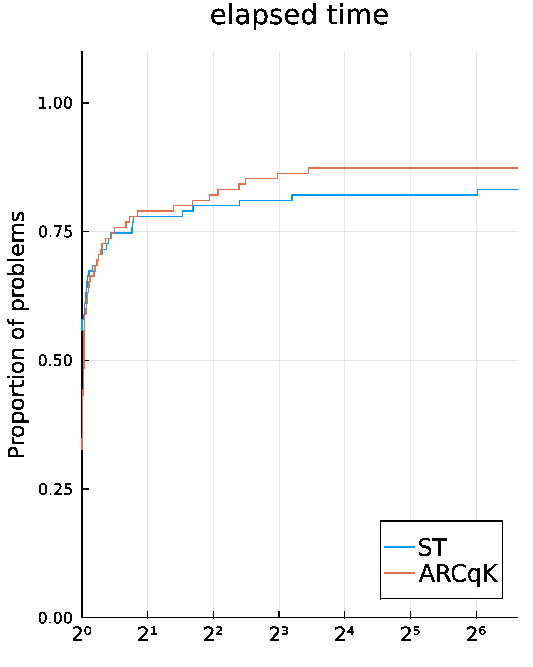
Our implementation is designed for large scale problems, so we expect to generalize these results to even larger problems.